Geometry
While we will be focusing more on topology, it is still important to dive slightly into geometry. As opposed to topology,geometry is the study of the properties of shapes that do change with bending and stretching. This can include lengths, angles, curvatures, and volume. Determining the geometric properties of a manifold can give us clues to the topology of the manifold. For 3-manifolds, there are 8 main types of geometries called “The Eight Thurston Geometries”.
- Euclidean
- Spherical
- Hyperbolic
- Nil
- SL(2,R)
- Sol
However, we will only discuss the first 3 geometries. This is because it is assumed that the universe is nearly perfectly isotropic and homogeneous. There will be resources on the website for anyone interested in reading more about the 8 geometric spaces.
Homogeneous vs Nonhomogeneous
A homogeneous manifold has the same geometric properties at every point in the manifold. This means that at any point in the manifold, it will look exactly the same as at every other point. In particular, the curvature is the same. A great example of a homogeneous manifold is the 2-sphere. At any point in the 2-sphere, it looks exactly the same as every other point on the 2-sphere.

A nonhomogeneous manifold is the opposite of a homogeneous manifold. There is at least one point in the manifold that does not have the same geometric properties as the rest of the manifold. An example could be the 2-Klein bottle pictured below, where at different points on the manifold, the curvatures are different. By simply having different curvatures at different points, we know that the manifold is nonhomogeneous.

Isotropic vs Anistropic
This property is a little more complicated. We will use 3-manifolds for examples. Let’s say we cut a solid ball in half vertically, what you see is a disk. Then cut the solid ball in half horizontally and what you see is also a disk. In both directions, vertically and horizontally, the shape still holds the same geometric properties. The directions are indistinguishable since the properties are the same in every direction. This is what makes a solid ball isotropic.

A shape or a space is anisotropic when you can distinguish between different directions. We will not focus on anisotropic shapes or spaces, but there will be resources with more information on the reference page.

Euclidean Space
Euclidean space is known for being a flat space, where the angle sum of a triangle will always equal 180. This is the most common plane that is taught. Think of high school geometry, it is typically geometry in the Euclidean plane. Because the plane does not curve at all, the curvature of the Euclidean plane is always exactly 0. In this space, the Pythagorean theorem is an important theorem that holds. For every right triangle with legs of length a and b and hypotenuse of length c, we have:

Spherical Space
Spherical space is known for being positively curved in that the angle sum of a triangle will always be greater than 180. This is because lines are arcs and curve outward. In this space, Pythagorean theorem no longer holds.
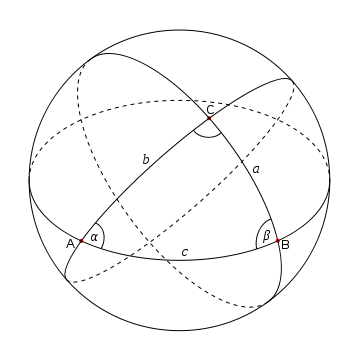
Hyperbolic Space
Hyperbolic space is negatively curved and the angle sum of a triangle is less than 180. To imagine a hyperbolic space, imagine a very wrinkly blanket that can never lay flat without overlapping. Another way that a hyperbolic space is represented is by a Poincaré disk model.



The Connection Between Topology and Geometry
In order to investigate the topology of the universe, there is a reason why it is important to introduce some basic information about geometry. Certain geometries can not have specific topologies, and vice versa. For example, any manifold that has a spherical geometry, can never be an infinite manifold, such as a plane. Therefore, if it was discovered that the universe is infinite, then we can automatically cross out any manifolds that have spherical geometries, such as a sphere and anything topologically equivalent to a sphere.
On the other hand, if we knew what geometry the universe has, then we can then cross out manifolds that can never have that geometry and its topologically equivalent manifolds. For example, if it is discovered that the universe has a Euclidean geometry, then that crosses out the possibility that the universe is a sphere. But it does not cross out possibilities of the universe being topologically a 3-torus, or Klein space.