What is CMB?
You may have heard someone say that when you look at the sky you are looking at the past. That is accurate and is what is helping researchers get information dating back to the big bang that occurred 13.8 billion years ago. Right after the big bang, the universe was too hot for atoms to form and consisted of plasma. About 380 hundred years later, the universe reached a cooler temperature that allowed the formation of atoms leaving photons nothing to interact with since electrons were now being pulled towards nuclei. These free-moving photons created Cosmic Microwave Background (CMB).
Why is the information from CMB so useful? Well, the speed of light is a finite number being roughly 3.00*10^8 m/s. Now this is important because this tells us that anything past 3.00^8 meters will take more than a second to arrive at its destination. Since the universe is quite large, light from distant points will take time to arrive on Earth. Let’s say for example you look at a star in the sky. The light we observe from the star may have taken hundreds of years to arrive on Earth. So there is a possibility that we are looking at a star that may not even exist anymore. CMB is similar in that when we are gathering information from the light it gives us, we are looking at light that took billions of light years to arrive, and thus is a way to look into the past and possibly figure out what the topology of the universe is.

There have been three satellites sent to space by NASA to gather data on CMB, the Cosmic Background Explorer (COBE) (1992), the Wilkinson Microwave Anisotropy Probe (WMAP) (2001-2010) and the Plank (2009-2013). Light from CMB arrives to earth from all directions and data has shown that they have nearly the same amount of energy. Using this model, researchers assume the universe we live in must have a nearly perfect homogeneous and isotropic geometry. The nearly perfect is important to note, because the evidence of our existence shows the universe is not perfectly homogeneous and isotropic:
“A perfectly homogeneous and isotropic universe expands to produce a perfectly homogeneous and isotropic universe. There would be no galaxies, no stars, no planets, and no cosmologists” p1466 (Cornish)
Matching Circles
One method researchers are attempting to use to gather evidence of a topology is by what is called “matching circles” or “circles-in-the-sky”. Researchers use a model of a 2-sphere with the earth at the center and the observed light from CMB originating on the surface of the 2-sphere. This sphere is called the “Last Scattering Surface”. The radius of the last scattering surface is called the “horizon radius”.

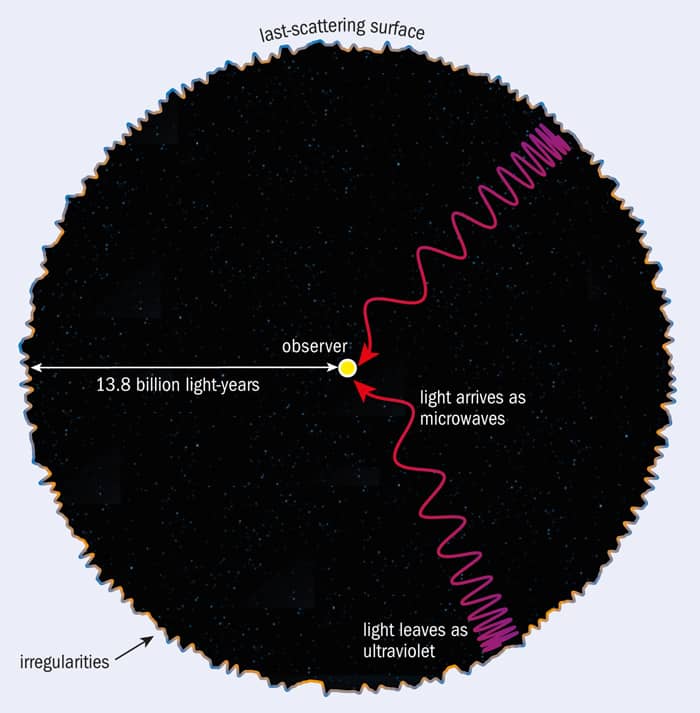
Surprisingly, there is evidence that the universe may be finite. But, why? Well, the data that is gathered from CMB is temperature fluctuations. These fluctuations reflect density fluctuation in the radiation. These fluctuations in temperature are expected and are the reason that we can conclude that the radiation is not perfectly homogenous. The problem arises in that satellites have confirmed that small fluctuations exist, but some of the larger fluctuations that would appear in an infinite universe are missing. Researchers have wondered what this means, and one of the possibilities is that the universe is smaller, and has a finite volume.
To understand the reasoning behind this, imagine you are holding your shoelace on both ends. If you were to try to create a wave like motion with your shoelace, there is a max length for that wave. The idea is similar for radiation being the wave, and the length of the universe being the shoelace.
For this reason, the matching circles is a possibility since we can assume a finite universe. To introduce the idea of matching circles, for the sake of simplicity, let’s say the universe is a 3-torus, which is a cube with its opposite faces glued together. Now if we cover all of the Euclidean space with these cubes, we get infinitely many 3-tori, that each encompass the universe. Each of these cubes is called a fundamental domain.

Now, within our universe is the last scattering surface. Thus in each 3-torus we also have the last scattering surface. Looking at the images below we have 2 possibilities:
- (a) The last scattering surface is smaller than the fundamental domain
- (b) The last scattering surface is larger than the fundamental domain
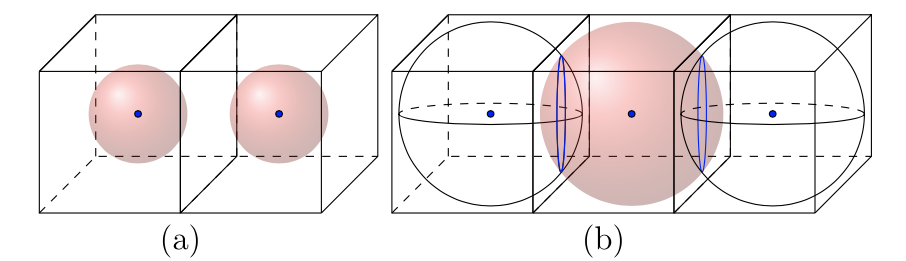
The hope for the matching circles method is that the last scattering surface is larger than the 3-torus. What would happen is that the last scattering surface would intersect itself. The points of intersection would form a circle which would be visible in the CMB radiation that can be seen by an observer. With any polyhedron, the opposite faces are glued together, thus whatever leaves from one face will come through its opposite face. Therefore as shown on image (b), the point of intersection will be shown on the 2 opposite faces, and we would see matching circles in opposite directions in the sky. This is the hope for the matching circles method. Researcher’s are aiming to find a pair of matching circles.